Cuando un fluido fluye por un conducto de diámetro variable, su velocidad cambia debido a que la sección transversal varía de una sección del conducto a otra.
En todo fluido incompresible, con flujo estacionario (en régimen laminar), la velocidad de un punto cualquiera de un conducto es inversamente proporcional a la superficie, en ese punto, de la sección transversal de la misma.
La ecuación de continuidad no es más que un caso particular del principio de conservación de la masa. Se basa en que el caudal (Q) del fluido ha de permanecer constante a lo largo de toda la conducción.
Dado que el caudal es el producto de la superficie de una sección del conducto por la velocidad con que fluye el fluido, tendremos que en dos puntos de una misma tubería se debe cumplir que:

Que es la ecuación de continuidad y donde:
- S es la superficie de las secciones transversales de los puntos 1 y 2 del conducto.
- v es la velocidad del flujo en los puntos 1 y 2 de la tubería.
Se puede concluir que puesto que el caudal debe mantenerse constante a lo largo de todo el conducto, cuando la sección disminuye, la velocidad del flujo aumenta en la misma proporción y viceversa.
Ejemplos:
1. Por el extremo de un tubo horizontal de 2 cm de diámetro ingresa agua a una velocidad de 0,2 m/s. ¿A qué velocidad saldrá el agua si el diámetro del extremo de salida es de 1 cm?
Solución:
Obtenemos los radios que son de 1 cm y 0,5 cm respectivamente. Luego calculamos las superficies de entrada y salida.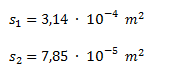
Por la ecuación de continuidad sabemos que el caudal (a · v) es constante a lo largo de todo el recorrido. Por lo tanto el caudal a la entrada debe ser igual al caudal a la salida.
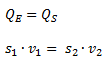
Despejamos la velocidad de salida de la ecuación de continuidad.
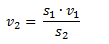
Reemplazamos por los valores y obtenemos el resultado.
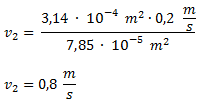
2. Por el extremo de un tubo de 5 cm de diámetro ingresa agua a una velocidad de 0,3 m/s. En el extremo de salida el agua sale a una velocidad de 0,6 m/s. ¿Cuál es el diámetro del extremo de salida?
Solución:
Calculamos el radio como la mitad del diámetro y nos da 2,5 cm. Luego calculamos la superficie de entrada:
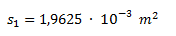
Planteamos la ecuación de continuidad.
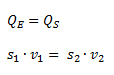
Despejamos la superficie de salida.
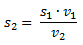
Reemplazamos por los valores del ejercicio
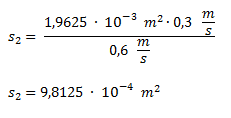
Pasamos el resultado a cm2. El número nos queda igual ya que por ser un superficie la coma se corre de a dos lugares a la vez. Por lo tanto de metros a centímetros debemos correrla cuatro lugares, que son los mismos lugares del exponente.
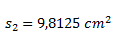
Planteamos la fórmula de la superficie de una circunferencia y despejamos el radio.
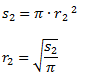
Reemplazamos los valores y obtenemos el radio.
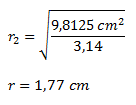
Luego el diámetro es igual al doble del radio, es decir 3,54 cm.
No hay comentarios:
Publicar un comentario